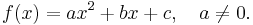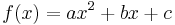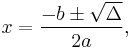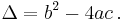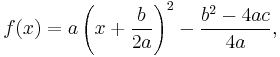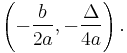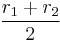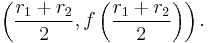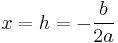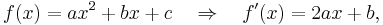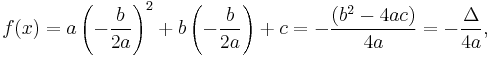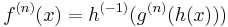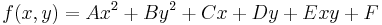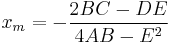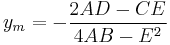Quadratic function
A quadratic function, in mathematics, is a polynomial function of the form
The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis.
The expression 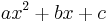 in the definition of a quadratic function is a polynomial of degree 2 or second order, or a 2nd degree polynomial, because the highest exponent of x is 2.
in the definition of a quadratic function is a polynomial of degree 2 or second order, or a 2nd degree polynomial, because the highest exponent of x is 2.
If the quadratic function is set equal to zero, then the result is a quadratic equation. The solutions to the equation are called the roots of the equation.
Contents |
Origin of word
The adjective quadratic comes from the Latin word quadrātum (“square”). A term like x2 is called a square in algebra because it is the area of a square with side x.
In general, a prefix quadr(i)- indicates the number 4. Examples are quadrilateral and quadrant. Quadratum is the Latin word for square because a square has four sides.
Roots
The roots (zeros) of the quadratic function
are the values of x for which f(x) = 0.
When the coefficients a, b, and c, are real or complex, the roots are
where the discriminant is defined as
Forms of a quadratic function
A quadratic function can be expressed in three formats:[1]
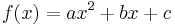 is called the standard form,
is called the standard form, is called the factored form, where
is called the factored form, where 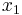 and
and 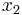 are the roots of the quadratic equation, it is used in logistic map
are the roots of the quadratic equation, it is used in logistic map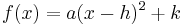 is called the vertex form, where h and k are the x and y coordinates of the vertex, respectively.
is called the vertex form, where h and k are the x and y coordinates of the vertex, respectively.
To convert the standard form to factored form, one needs only the quadratic formula to determine the two roots 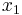 and
and 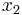 . To convert the standard form to vertex form, one needs a process called completing the square. To convert the factored form (or vertex form) to standard form, one needs to multiply, expand and/or distribute the factors.
. To convert the standard form to vertex form, one needs a process called completing the square. To convert the factored form (or vertex form) to standard form, one needs to multiply, expand and/or distribute the factors.
Graph
Regardless of the format, the graph of a quadratic function is a parabola (as shown above).
- If
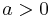 (or is a positive number), the parabola opens upward.
(or is a positive number), the parabola opens upward. - If
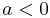 (or is a negative number), the parabola opens downward.
(or is a negative number), the parabola opens downward.
The coefficient a controls the speed of increase (or decrease) of the quadratic function from the vertex, bigger positive a makes the function increase faster and the graph appear more closed.
The coefficients b and a together control the axis of symmetry of the parabola (also the x-coordinate of the vertex) which is at 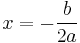 .
.
The coefficient b alone is the declivity of the parabola as y-axis intercepts.
The coefficient c controls the height of the parabola, more specifically, it is the point where the parabola intercept the y-axis.
Vertex
The vertex of a parabola is the place where it turns, hence, it's also called the turning point. If the quadratic function is in vertex form, the vertex is 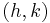 . By the method of completing the square, one can turn the general form
. By the method of completing the square, one can turn the general form
into
so the vertex of the parabola in the vertex form is
If the quadratic function is in factored form
the average of the two roots, i.e.,
is the x-coordinate of the vertex, and hence the vertex is
The vertex is also the maximum point if 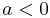 or the minimum point if
or the minimum point if 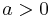 .
.
The vertical line
that passes through the vertex is also the axis of symmetry of the parabola.
Maximum and minimum points
Using calculus, the vertex point, being a maximum or minimum of the function, can be obtained by finding the roots of the derivative:
giving
with the corresponding function value
so again the vertex point coordinates can be expressed as
The square root of a quadratic function
The square root of a quadratic function gives rise either to an ellipse or to a hyperbola.If 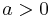 then the equation
then the equation 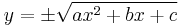 describes a hyperbola. The axis of the hyperbola is determined by the ordinate of the minimum point of the corresponding parabola
describes a hyperbola. The axis of the hyperbola is determined by the ordinate of the minimum point of the corresponding parabola 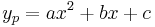 .
.
If the ordinate is negative, then the hyperbola's axis is horizontal. If the ordinate is positive, then the hyperbola's axis is vertical.
If 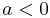 then the equation
then the equation 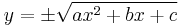 describes either an ellipse or nothing at all. If the ordinate of the maximum point of the corresponding parabola
describes either an ellipse or nothing at all. If the ordinate of the maximum point of the corresponding parabola 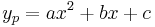 is positive, then its square root describes an ellipse, but if the ordinate is negative then it describes an empty locus of points.
is positive, then its square root describes an ellipse, but if the ordinate is negative then it describes an empty locus of points.
Iteration
Given an 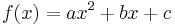 , one cannot always deduce the analytic form of
, one cannot always deduce the analytic form of 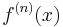 , which means the nth iteration of
, which means the nth iteration of  . (The superscript can be extended to negative number referring to the iteration of the inverse of
. (The superscript can be extended to negative number referring to the iteration of the inverse of  if the inverse exists.) But there is one easier case, in which
if the inverse exists.) But there is one easier case, in which 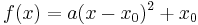 .
.
In such case, one has
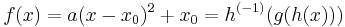 ,
,
where
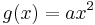 and
and 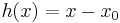 .
.
So by induction,
can be obtained, where 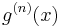 can be easily computed as
can be easily computed as
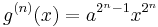 .
.
Finally, we have
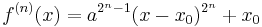 ,
,
in the case of 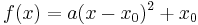 .
.
See Topological conjugacy for more detail about such relationship between f and g. And see Complex quadratic polynomial for the chaotic behavior in the general iteration.
Bivariate (two variable) quadratic function
A bivariate quadratic function is a second-degree polynomial of the form
Such a function describes a quadratic surface. Setting 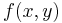 equal to zero describes the intersection of the surface with the plane
equal to zero describes the intersection of the surface with the plane 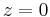 , which is a locus of points equivalent to a conic section.
, which is a locus of points equivalent to a conic section.
Minimum/maximum
If 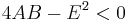 the function has no maximum or minimum, its graph forms an hyperbolic paraboloid.
the function has no maximum or minimum, its graph forms an hyperbolic paraboloid.
If 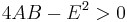 the function has a minimum if A>0, and a maximum if A<0, its graph forms an elliptic paraboloid.
the function has a minimum if A>0, and a maximum if A<0, its graph forms an elliptic paraboloid.
The minimum or maximum of a bivariate quadratic function is obtained at 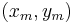 where:
where:
If 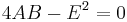 and
and 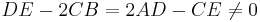 the function has no maximum or minimum, its graph forms a parabolic cylinder.
the function has no maximum or minimum, its graph forms a parabolic cylinder.
If 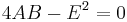 and
and 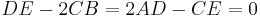 the function achieves the maximum/minimum at a line. Similarly, a minimum if A>0 and a maximum if A<0, its graph forms a parabolic cylinder.
the function achieves the maximum/minimum at a line. Similarly, a minimum if A>0 and a maximum if A<0, its graph forms a parabolic cylinder.
See also
- Quadratic form
- Quadratic equation
- Quadratic polynomial
- Matrix representation of conic sections
- Quadric
- Periodic points of complex quadratic mappings
- List of mathematical functions
References
- ^ Hughes-Hallett, Deborah; Connally, Eric; McCallum, William G. (2007), College Algebra, John Wiley & Sons Inc, p. 205, ISBN 0471271756, 9780471271758, http://books.google.be/books?sourceid=navclient&ie=UTF-8&rlz=1T4GGLJ_enBE306BE306&q=%22three+different+forms+for+a+quadratic+expression+are%22, Search result
External links
- Weisstein, Eric W., "Quadratic" from MathWorld.
|
||||||||